Teorema di unicità del limite
Se per x che tende a x0 la funzione f(x) ha per limite l , allora tale limite è unico.
Dimostrazione:
Supponiamo per assurdo che la funzione abbia due limiti l1 ed l2. Allora se scelgo
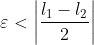
non possono verificarsi contemporaneamente
<&space;l_1+\varepsilon)
<&space;l_2+\varepsilon)
nel disegno sottostante si è scelto ε minore si |l1-l2|/2 si vede che i due intervalli (l1-ε,l1+ε) e (l2-ε,l2+ε) sono disgiunti e quindi non possono verificarsi contemporaneamente le due relazioni di sopra

Teorema di permanenza del segno
Se la funzione f(x) per x che tende a x0 tende ad un valore l da zero allora esiste un intorno completo di x0 escluso al pi x0, in cui la funzione assume lo stesso valore di l .
Dimostrazione:basta prendere ε<|l| pertanto esiste un intorno in cuise l<0 l-ε< f(x)< l+ε<0 in quanto per ipotesi l+ε<0, perciò la f(x)<0se l>0 0<l-ε< f(x)< l+ε in quanto per ipotesi l-ε>0, perciò la f(x)>0Di conseguenza la f(x) in tale intorno assume sempre lo stesso segno escluso al più x0
Teorema del confronto
Se le funzioni g(x) ed h(x) per x che tende ad x0 tendono allo stesso valore e in un intorno completo di x0 escluso al più x0, si ha
\leq&space;f(x)\leq&space;h(x))
allora anche la f(x) tende ad l
Dimostrazione:
poiché fissato ε esiste un intoro di x0, in cui l-ε< g(x)< l+ε e l-ε< h(x)< l+ε quindi per l'ipotesi l-ε< g(x)<f(x)<h(x)< l+ε di conseguenza f(x) tende ad l
Teorema di unicità del limite
Supponiamo che
=m) |
e |
=l) |
allora
![\lim_{x\rightarrow x_0}[f(x)+ g(x)]=l+ m](https://latex.codecogs.com/gif.latex?\lim_{x\rightarrow&space;x_0}[f(x)+&space;g(x)]=l+&space;m)
Quando non tutti e due i limiti sono finiti si possono presentare i seguenti casi:
- uno dei due è finito diverso da zero e l'altro infinito il limite vale infinito;
- tutti e due limiti valgono infinito allora il limite vale infinito;
- un limite vale no dei due vale +∞ e l'altro -∞ si ha una {tooltip class="tooltips tooltips-effect-5"}forma indeterminata{end-link} Caso in cui non è possibile ricavare il limite della funzione composta dai limiti di ciascuna singola funzione{end-tooltip} +∞-∞
Dimostrazione : in allestimento
Il tuo testo...




