Data l'equazione Ax2+Bx+c=0
Poiché il termine di secondo grado deve essere presente A non può annullarsi, quindi possono presentarsi i seguenti casi:
- B=0 e C=0 equazione monomia
- C=0 equazione spuria
- B=0 equazione pura
EQUAZIONE MONOMIA
L'equazione ha la forma Ax2=0, pertanto x2=0/A cioè x=0, di conseguenza un'equazione monomia ha una radice nulla
EQUAZIONE SPURIA
L'equazione ha la forma Ax2+Bx=0, posto x in evidenza si ottiene x(Ax+B)=0 essendo un prodotto uguale a zero allora, per la legge di annullamento del prodotto, almeno uno dei due fattori è zero,cioè si ha
x=0 o Ax+B=0 .
Si è ricondotta l'equazione di secondo grado alla risoluzione di due equazioni di primo, di cui una ha soluzione nulla.
L'altra soluzione è 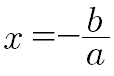
In questo abbiamo una equazione con due soluzioni sicuramente distinte di cui una è lo zero.
EQUAZIONE PURA
L'equazione ha la forma Ax2+C=0 che si può scrivere nella forma Ax2=-C, pertanto
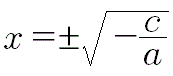
Il primo membro è sicuramente non negativo poiché è un quadrato allora deve esserlo anche il secondo membro. Se A e C sono concordi il secondo membro è negativo in quanto la frazione è preceduta dal segno meno, di conseguenza non si hanno radici, reali essendo il primo membro positivo. Se invece A e C sono discordi si hanno due radici reali opposte che si ottengono
{

