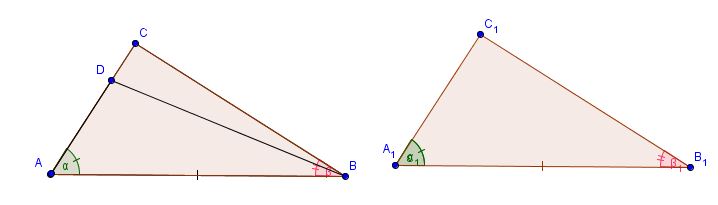
Teorema: Se due triangoli hanno congruenti rispettivamente due angoli e il lato ad essi adiacente allora sono congruenti.

| Ipotesi | Tesi | |
| |
======> | |
Dimostrazione:
Supponiamo per assurdo che date le ipotesi i due triangoli non siano congruenti. Supponiamo che AC non sia congruente ad A1C1, supponiamo che AC>A1C1 quindi esisterà un punto D in AC tale che quindi poichè valgono le ipotesi del primo criterio di congruenza
ma questo non è possibile in quanto
.
Pertanto l'ipotesi fatta sulla non congruenza è falsa, e quindi i due triangoli sono congruenti.