Teorema: Se due triangoli hanno congruenti rispettivamente tre  lati  allora sono congruenti.

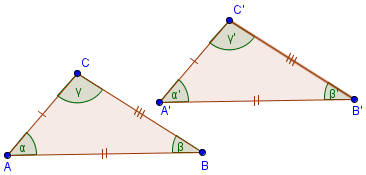
Ipotesi	Tesi

Dimostrazione:

poichè 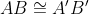 esiste un movimento rigido che sovvrappone AB con A'B', viene fatta una simmetria rispetto ad AB, il punto C finisce dalla parte opposta di C' rispetto ad AB.

I triangoli della figura sottostante sono acutangoli, ma i ragionamenti che si faranno si adattano anche al caso dei triangoli ottusangoli.La figura sottostante è uOra si deve dimostrare che i due triangoli della figura sottostante sono congruenti.

Si noti che i triangoli di questa figura sono acuti, stesso considerazioni ch

Il triangolo A'CC' è isoscele quindi per  {modal /geometria/geometria-euclidea/91-i-triangoli/262-il-teorema-del-triangolo-isoscele}il teorema del triangolo isoscele{/modal} gli angoli alla base CC' sono congruenti, stesso discorso vale per il triangolo B'CC', anche in questo caso gli angoli alla base sono congruenti. pertanto gli angoli in C e C' essendo somma di angoli congruenti sono congruenti.

Di conseguenza i due triangoli ABC e A'B'C' hanno almeno due lati congruenti e l'angolo fra essi compreso. Per il primo criterio di congruenza sono congruenti

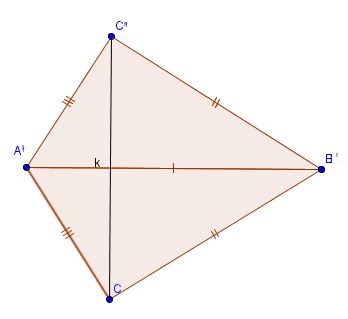
In questo movimento rigido poiché  il  punto B si sovrappone a B'. Allo stesso modo poiché  il punto C si sovrappone al punto C'.

Pertanto i tre vertici si sovrappongono e quindi i due triangoli sono congruenti.