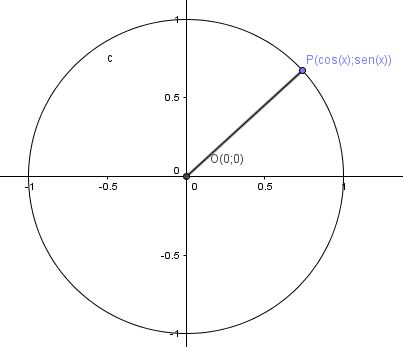
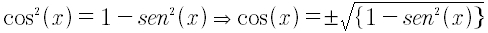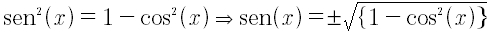Si consideri il punto P(cos(x);sen(x)) appartenente alla circonferenza goniometrica di equazione
![]() .
.
Questo punto verifica la condizione di appartenenza e quindi sostituendo le coordinate del punto nell'equazione si verifica questa relazione
![]()
che prende il nome di relazione fondamentale della goniometria, detta anche prima relazione della goniometria.
Da questa si ottengono due relazioni inverse
Per ogni valore di sen x si ottengono due valori di cos x , uno col segno più ed uno col segno meno.
Il segno dipende dal quadrante in cui si trova l'angolo