Si chiama circonferenza goniometrica una circonferenza avente il centro nell'origine degli assi cartesiani e raggio uguale ad uno.
L'equazione generica di una circonferenza nel piano cartesiano è x2+y2+ax+by+c=0
dove a=-2a b= -2b c=a2+b2-r2 pertanto nel caso della circonferenza goniometrica è
x2+y2=1

Il punto A(1;0) è detto origine degli angoli, ad ogni punto P resta associato l'angolo AOP. Per convenzione gli angoli percorsi in senso antiorario sono positivi, negativi se percorsi insenso orario.
Si realizza una corrispondenza fra gli angoli e i punti della circonferenza goniometrica evidenziata dalla tabella sottostante
Angolo |
Punto |
0 |
(1;0) |
90° |
(0;1) |
180° |
(-1;0) |
270° |
(0;-1) |
360 |
(1;0) |
-90° |
(0;-1) |
-180° |
(-1;0) |
L'unità di misura degli angoli è il grado sessagesimale, che è definito come la trencentosessasentesima parte di un angolo giro. In goniometria si utilizza una seconda unità di misura che prende il nome di radiante.
Definizione: il radiante è la misura di un angolo ed è pari il rapporto tra la lunghezza dell'arco sotteso dall'angolo ed il raggio della circonferenza.
Nel caso della circonferenza gonimetrica in cui il raggio vale uno, la misura un radianti è uguale alla lunghezza dell'arco sotteso.
La lunghezza della circonferenza goniometrica è uguale a 2P , pertanto l'angolo giro corrisponde a a 2P. L'angolo piatto, che vale 180 gradi in radianti corrisponde a P radianti.
Indichiamo con a l'angolo in radianti, con a°. Vale la proporzione
a:a°=P:180°
Di conseguenza applicando la relazione fondamentale delle proporzione, cioè il prodotto degli estremi è uguale al prodotto degli estremi,
a*180°=a°*P
si ottengono le relazioni fra gradi e radianti
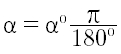
e
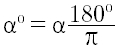
La tabella sottostante indica la relazione fra gradi e radianti
| Gradi | Radianti |
| 0° | 0 |
| 30° | P/6 |
| 45° | P/4 |
| 60° | P/3 |
| 90° | P/2 |
| 180° | P |
| 360° | 2P |

