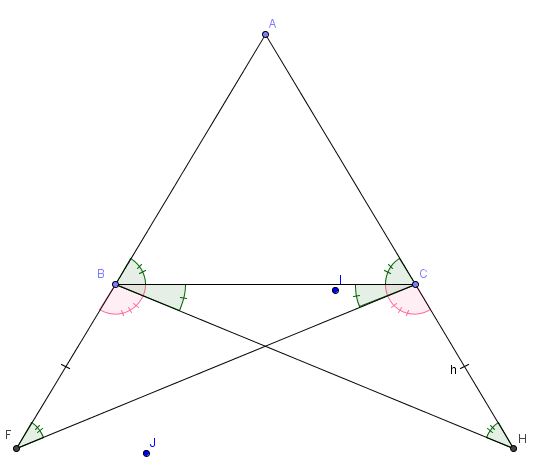
Teorema: un triangolo isoscele ha gli angoli alla base congruenti
Ipotesi => Tesi
Dimostrazione: consideriamo la bisettrice AH, i due triangoli ABH e AHC hanno due lati congruenti e l'angolo fa essi compresi quindi per il primo criterio di congruenza sono congruenti.
Pertanto sono congruenti anche gli angoli in B ed in C, come volevasi dimostrare.
Dal teorema si deduce che quindi H è il punto medio di BC e quindi la bisettrice è anche mediana.
Nei due triangoli AHB e AHC gli angoli in H sono congruenti e supplementari quindi sono retti, pertanto AH è anche altezza.
Un teorema inverso è quello che si ottiene dal teorema diretto scambiando l'ipotesi con la tesi.
In quest caso vale il è vero il teorema inverso.
Pertanto si ha il seguente teorema
Teorema inverso: un triangolo che ha gli angoli alla base congurenti è isoscele
Ipotesi => Tesi
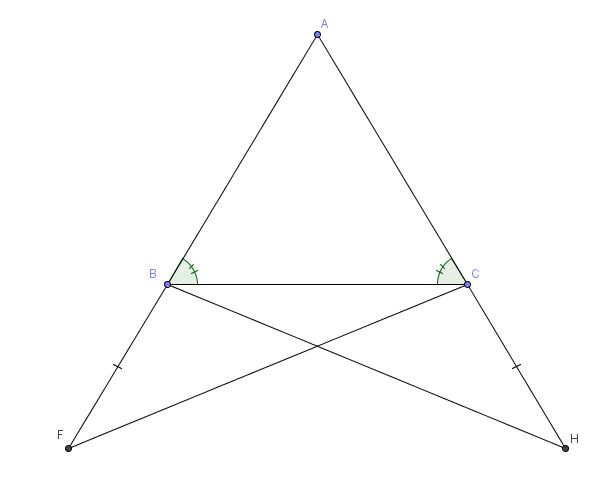
. Poichè per ipotesi
, gli angoli
e
sono congruenti in quanto supplementari agli angoli alla base.
Quindi i triangoli FBC e HCB sono congruenti per il primo criterio poichè hanno congruenti due lati e l'angolo fra essi compreso e il lato ad esso adiacente.
Di conseguenza sono congruenti anche i triangoli ACF ABH per il secondo criterio, Quindi essendo lati corrispondenti sdei due triangoli congruenti. I lati AB e BC sono conruenti perche differenzè di lati congruenti.