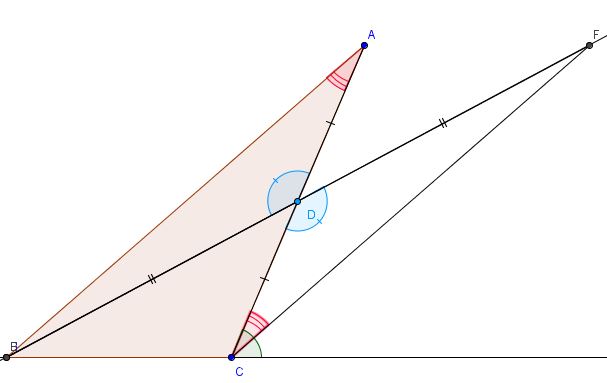
Teorema: in un triangolo, un'angolo esterno è maggiore di ciascuno degli angoli interni non adiacenti

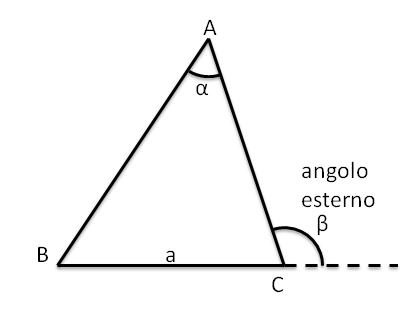
Ipotesi:   ABC è un trianglo qualunque

Tesi:      

Consideriamo il punto medio D del lato AC, si FD il prolungamento del segmento BD ad esso equivalente.

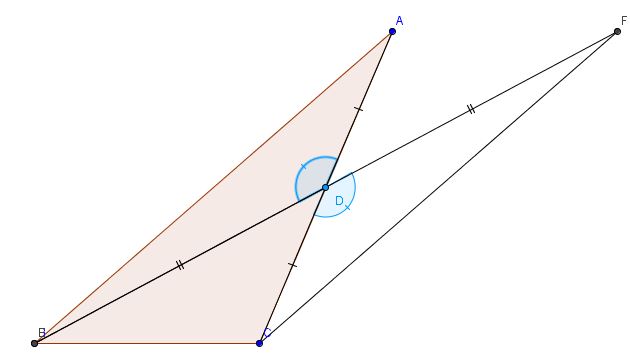
I triangoli BDC  e CDF sono equivalenti per il primo criterio di congruenza, avendo due lati congruenti e l'angolo fra essi compreso.

Di conseguenza . Quest'ultimo angolo è una parte dell'angolo esterno pertanto

da cui si ottiene la tesi.

Allo stesso modo si può dimostrare che anche l'altro angolo intero non adiacente è minore dell'angolo esterno.