Si vuole ricavare la formula risolutiva dell'equazione di secondo grado completa.
In primo luogo si trasporta il termine noto c al secondo membro
ax2+bx=-c
Si moltiplica per 4a entrambi i membri, ottenendo:
-
4a2x2+4abx=-4ac
Si osservi che 4a2x2=(2ax)2 e 4abx =2·(2ax)·b
cioè al primo membro il primo termine è il quadrato di un monomio, mentre il secondo termine è il doppio prodotto di 2ax e b
si aggiunge b2 al primo ed al secondo membro in modo da avere al primo membro il quadrato del binomio 2ax+b.
4a2x2+4abx+b2=b2-4ac cioè (2ax+b)2=b2-4ac.
Estraendo la radice quadrata ad ambo i membri si ottiene
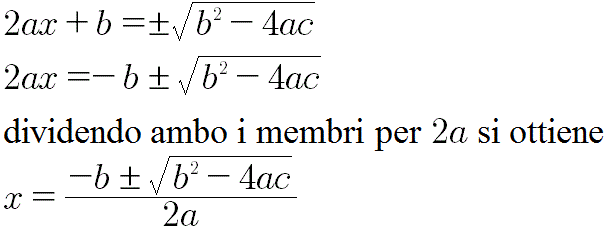
Affinchè le soluzioni siano reali occorre che il radicando non sia negativo.
Questo radicando b2-4ac si chiama discriminante dell'equazione di secondo grado e si indica con la lettera Δ
A seconda del valore di Δ si possono presentare tre casi:
- Δ>0 le soluzioni sono reali e distinte
- Δ=0 soluzioni reali e coincdenti
- Δ<0 soluzioni immaginarie
In determinate situazioni è possibile trovare le soluzioni senza applicare la formula risolutiva.
Dalla formula risolutiva si deducono le seguenti relazioni:
- la somma delle soluzioni x1+x2 è uguale a -b/a
- il prodotto x1·x2 delle soluzioni è uguale a c/a
In particolare quando a=1 e le soluzioni sono numeri interi, per trovare le soluzioni si possono utilizzare queste due relazioni.
Esempio: data l'equazione
x2-3x-4=0 ha due soluzioni la cui somma vale -b/a=3/1=3 ed il cui prodotto vale c/a=-4/1=-4,
di conseguenza i due numeri sono 4 e -1 perchè la loro somma vale 3 ed il cui prodotto vale -4

