Supponiamo di dover risolvere la disequazione di secondo grado ax2+bx+c <0,
Se il trinomio ax2+bx+c possiede zeri distinti se il D>0 . In questo caso, indicato con x1 e x2 tali zeri il trinomio si scompone come
a(x-x1)(x-x2)
pertanto per risolvere una disequazione si deve studiare il segno del trinomio, per fare ciò occorre confrontare i segni dei tre fattori a, x-x1,x-x2
Il segno di x-x1 dipende dal valore di x, e si studia imponendo x-x1>0, quindi questo fattore è positivo per x>x1, negativo in caso contrario.
Stesso ragionamento per x-x2.
Il segno del prodotto si studia mediante un grafico che riporta i segni dei singoli fattori
| a>0 | a<0 | |
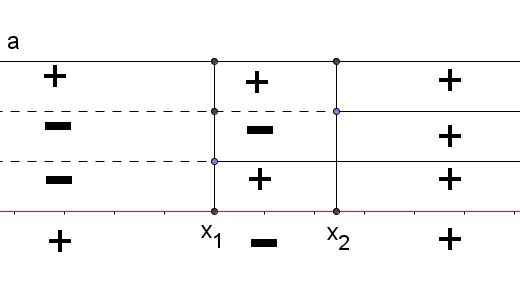 |
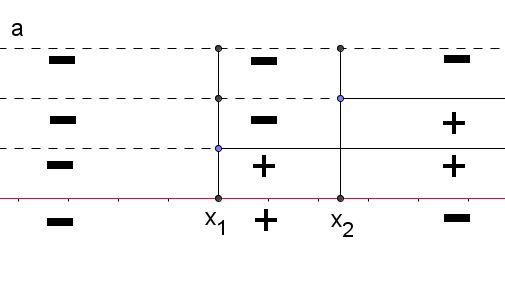 |
Le soluzioni vanno ricercate negli intervalli in cui il segno corrisponde la verso della disequazione,
Per esempio se a>0 ed il verso è maggiore le soluzioi sono per valori esterni, cioè x<x1 oppure x>x2.
Se D<0 . Il segno del trinomio è lo stesso del coefficiente a del termine di secondo grado, pertanto se a e il verso della disequazione sono concordi la disequazione è sempre verificata, mai se sono discordi.
Le soluzioni che si che si ottengono naturalmente sono le stesse xhe si ottengono usando il metodo grafico.

