Supponiamo di dover risolvere la disequazione di secondo grado ax2+bx+c <0,
Si considera la parabola y=ax2+bx+c , essendo il verso della disequazione minore, la ricerca delle soluzioni è equivalente a trovare sull'asse ascisse, quelle x per i quali le corrispondenti ordinate y=ax2+bx+c dei punti della parabola sono negative. Analoghe considerazioni si fanno se il verso è maggiore.
Occorre quindi rappresentare, non necessariamente in maniera precisa la parabola y=ax2+bx+c
Le caratteristiche fondamentali che bisogna individuare sono due:
- la concavità della parabola, che si determina con il segno del coefficiente a del termine di secondo grado.
- è verso l'alto se a>0;
- versoil basso se a<0;
- l'esistenza di eventuali intersezioni con gli assi.
- due intersezioni distinte se Δ>0;
- nessuna soluzione se Δ<0;
- due soluzioni coincidenti se Δ=0.
Per individuare le soluzioni della disequazioe occorre disegnare la parabola sulla base delle precedenti caratteristiche.
Le soluzioni corrispondono ai valori di x dei punti le cui ordinate hanno un segno che coincide col verso della disequazione.
La seguente tabella ci permette di distinguere i vari casi.
| verso della disequazione---------------> |
> |
≥ |
< |
≤ |
||
| D>0 | a>0 | 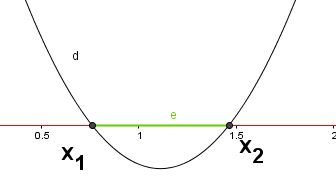 |
soluzioni per valori esterni x<x1 ν x>x2 |
soluzioni per valori esterni x≤x1 ν x≥x2 |
soluzioni per valori interni
x1<x<x2 |
soluzioni per valori interni x1≤x≤x2 |
| D>0 | a<0 | 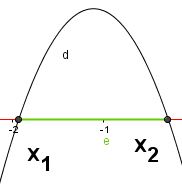 |
soluzioni per valori interni
x1<x<x2 |
soluzioni per valori interni
x1<x<x2 |
soluzioni per valori esterni x<x1 ν x>x2 |
soluzioni per valori esterni x≤x1 ν x≥x2 |
| D=0 | a>0 | 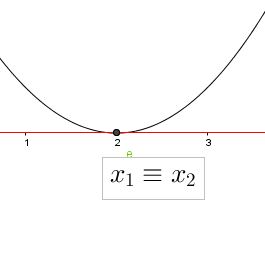 |
x≠x1 | sempre verificata | mai verificata | x=x1 |
| D=0 | a<0 | 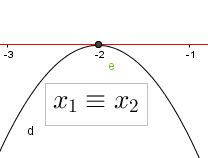 |
mai verificata | x=x1 | x≠x1 | sempre verificata |
| D<0 | a>0 | 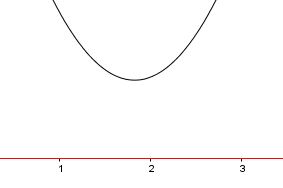 |
sempre verificata | sempre verificata | mai verificata | mai verificata |
| D<0 | a<0 | 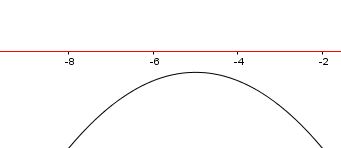 |
mai verificata | mai verificata | sempre verificata | sempre verificata |
Metodo grafico con geogebra

