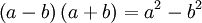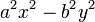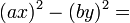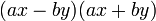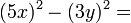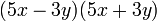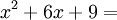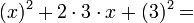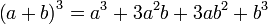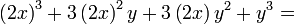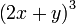Usando i meccanismi inversi dei prodotti notevoli è possibile scomporre in fattori alcuni polinomi.
DIFFERENZA FA DUE QUADRATI
Si può utilizzare l'inverso del prodotto notevole:
Consideriamo questo polinomio:
In questo caso notiamo che ogni {tooltip class="tooltips tooltips-effect-4"}monomi{end-link}prodotto di numeri e lettere{end-tooltip}o è un quadrato perfetto. Riscriviamo dunque il polinomio in un'altra forma:
Noteremo quindi che questo polinomio non è altro che il prodotto notevole della differenza di due quadrati.
Facciamo un altro esempio:
QUADRATO DI UN BINOMIO
Si può utilizzare l'inverso del prodotto notevole:
Consideriamo questo trinomio:
poiché si possono individuare i quadrati di due {tooltip class="tooltips tooltips-effect-4"}monomi{end-link}prodotto di numeri e lettere{end-tooltip} e il loro doppio prodotto:
il trinomio di partenza è equivalente a:
CUBO DI BINOMIO
Si può utilizzare l'inverso del prodotto notevole:
Consideriamo questo quadrinomio:
poiché si possono individuare i due cubi e i due tripli prodotti:
il quadrinomio di partenza è equivalente a:
Analogamente: