Semiretta
SEMIRETTA
la parte di retta costituita da un punto di essa, detto origine della semiretta, e da tutti i punti che stanno dalla stessa parte rispetto all’origine.

Segmento
SEGMENTO
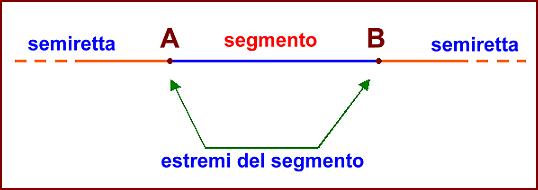
è l’insieme costituito da A, B e tutti i punti compresi tra A e B. I punti A,B sono detti estremi del segmento. Se A e B coincidono il segmento si dice nullo.
Segmenti consecutivi
SEGMENTI CONSECUTIVI

sono due segmenti che hanno in comune SOLO un estremo si dicono consecutivi
Segmenti adiacenti
SEGMENTI ADIACENTI
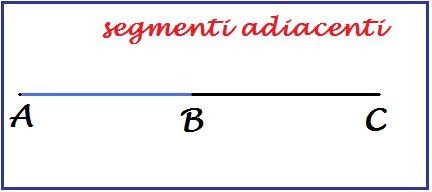
sono due segmenti consecutivi che appartengono alla stessa retta.
Angolo
ANGOLO
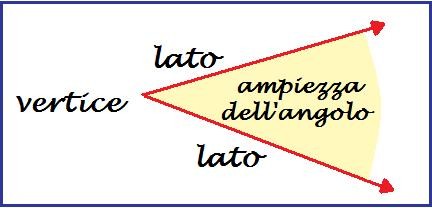
è ciascuna delle due{tooltip class="tooltips tooltips-effect-5"}figure geometriche{end-link}Insieme di punti {end-tooltip} delimitate da due semirette aventi la stessa {tooltip class="tooltips tooltips-effect-6"}origine{end-link}punto che precede tutti i punti della semiretta{end-tooltip}
Spezzata
SPEZZATA
Si definisce spezzata una figura geometrica formata da un'insieme di segmenti che hanno in comune un estremo.
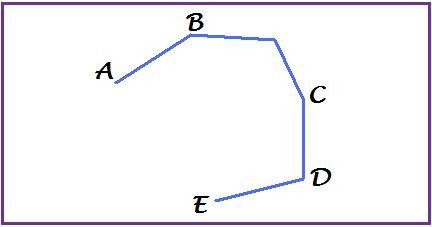
La spezzata si dice chiusa se il primo estremo del primo {tooltip class="tooltips tooltips-effect-5"}segmento{end-link}Insieme dei punti di una retta delimitati da due punti detti estremi{end-tooltip} segmento coincide col secondo estremo dell'ultimo segmento, aperta in caso contrario.
Una spezzata in cui solo due segmenti hanno in comune un punto che non sia un estremo si dice intrecciata.
Una spezzata chiusa non intrecciata prende il nome di poligonale
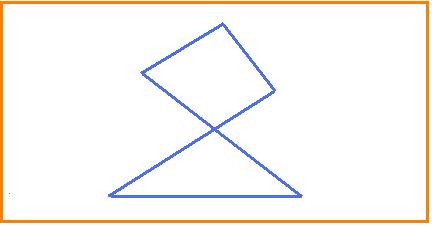 Esempio di spezzata chiusa intrecciata
Esempio di spezzata chiusa intrecciata

poligonale
Si chiama poligono la parte di piano delimitata da una poligonale









 Esempio di spezzata chiusa intrecciata
Esempio di spezzata chiusa intrecciata


/Immagini/Figura%204_2.gif)