I limiti notevoli sono particolari limiti che si presentano frequentemente e che permettono di risolvere forme indeterminate di altri limiti.
I più usati sono:
| 1) | 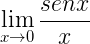 =1 =1 |
| 2) | 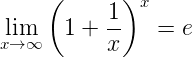 |
| 3) | 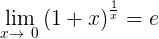 |
| 4) | 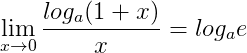 |
| 5) |
Limite 1
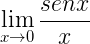 =1
=1
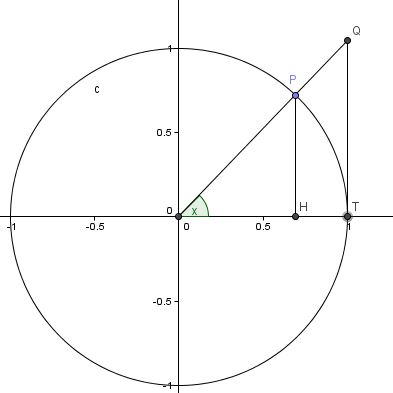
Dalla figura osserviamo che 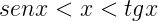 poiche il segmento PH è minore dell'arco x . Dividendo i termini per sen x si ottiene
poiche il segmento PH è minore dell'arco x . Dividendo i termini per sen x si ottiene

semplificando
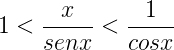
invertendo i termini della disuguaglianza
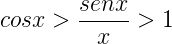
Sia il primo che il terzo termine tendono a 1 , pertanto si ha
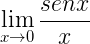 =1
=1
Limite 2
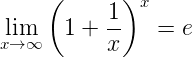
Si definiscono le due successioni

La successione an è crescente, per mostrarlo si scrive nella forma
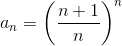
quindi
per la disuguaglianza di Bernoulli (1+x)n>1+nx al numeratore
Analogamente si mostra che bn è decrescente.
an<bn infatti
poichè b1=4 e bn è decrescente an è sicuramente minore di 4, quindi essendo limitata superiormente e crescente avrà sicuramente un limite a cui si attribuisce il simbolo e ed è chiamato numero di Nepero, ha il valore pari a 2,7188.
Si osservi che anche la successione bn tende ad e infatti
Dimostriamo ora che
supponiamo che n=[x] siala parte intera di x
vale la seguente disuguaglianza
La prima parte della disuguaglianza deriva dal fatto che [x]+1>x e si trova al denominatore, mentre la seconda scaturisce dal fatto che [x]<x sempre al denminatore, menrtre l'esponente [x]+1>x e la base è maggiore di uno.
il primo membro della disuguaglianza tende ad e infatti il numeratore tende ad e mentre il denominatore tende a 1, il terzo membrio è proprio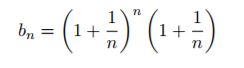
Pertanto per il teorema del confronto 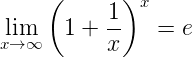
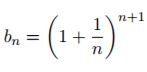
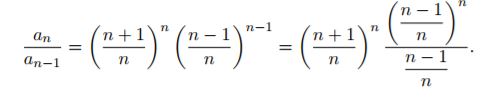
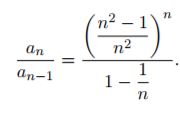
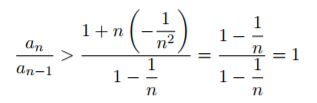
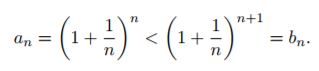
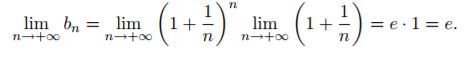
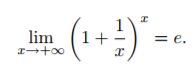
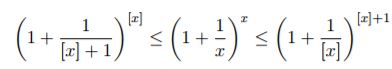
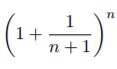
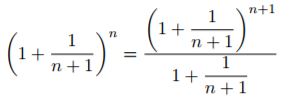
.gif) ..
...gif)