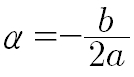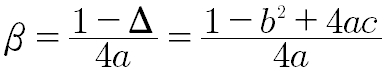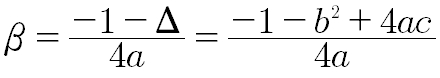Condizione per determinare l'equazione

L'equazione della parabola dipende da tre parametri a,b,c, pertanto occorre trovare tre codizioni indipendenti per determinarla.

Per trovare a,b,c si risolve il sistema formato dalle tre equazioni determinate dalle tre condizioni.

In certi casi le condizioni danno luogo ad equazioni di secondo grado

Condizione nota	Come si applica
Appartenenza alla parabola	condizione di appartenenza
ascissa del fuoco o vertice	$\mathbf{{ si \; \; \; \; pone}} \; \; \; \; \; \alpha =-\frac{b}{2a}$
ordinata del fuoco	$\mathbf{{ si \; \; \; \; pone}} \; \; \; \; \; \beta =\frac{1-\Delta}{4a}\; \; \; \mathbf{con} \; \; \; \Delta =b^2-4ac$
equazione direttrice y=d	$\mathbf{{ si \; \; \; \; pone}} \; \; \; \; \; d =\frac{-1-\Delta}{4a}\; \; \; \mathbf{con} \; \; \; \Delta =b^2-4ac$
equazione dell'asse x=α	$\mathbf{{ si \; \; \; \; pone}} \; \; \; \; \; \alpha =-\frac{b}{2a}$
vertice	corrisponde a due condizioni $\mathbf{{ si \; \; \; \; pone}} \; \; \; \; \; \alpha =-\frac{b}{2a}$ la condizione di appartenenza
tangente e punto di tangenza	corrisponde due condizioni: condizione di appatenenza del punto di tangenza m=2ax₀+b con m coefficiente angolare tangente

Condizioni per determinare l'equazione