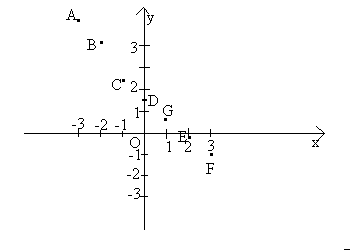Un sistema di equazioni lineari è costituito da più equazioni con diverse incognite che compaiono tutte con gradi uno.
Def.Si chiama soluzione di un sistema di equazioni la coppia ordinata di numeri che sostituita al posto delle incognite verifica entrambe le equazioni.
Due sistemi che hanno le stesse soluzioni si dicono equivalenti
Un sistema di equazioni è scritta a forma normale se in ogni equazione le incognite compaiono nello stesso ordine al primo membro, mentre i termini senza incognita (termini noti) sono scritti al secondo membro, in ogni caso si può sempre scrivere a forma normale trasportando i termini con le incognite al primo membro gli altri al secondo.
Per ricavare le soluzioni di una equazione 5x+6y-=0 occorre isolare ( o esplicitare) una delle due incognite, come se l'altra incognita fosse un numero.
Per esempio isolando la y si ottiene y=(-5x+9)/6, pertanto attribuendo un valore arbitrario alla x si ricava il corrispondente valore della y, quindi se x=1 allora y=(-5*1+9)/6=2/3. La coppia (1,2/3) sarà una soluzione del sistema.Poichè la x viene scelta in infiniti modi infinite saranno le soluzioni.Si costruisce una tabella con due colonne, nella prima scegliamo in maniera arbitraria i valori della x, nell'altra il corrispondente valore della y
Un sistema di equazioni lineari può essere risolto con diversi metodi.
| x | y | soluzione dell'equazione |
|
| -3 |
(-5*(-3)+9)/6= 4 |
A(-3,4) |
|
| -2 |
(-5*(-2)+9)/6= 19/6 |
B(-2,19/6) |
|
| -1 |
(-5*(-1)+9)/6= 7/3 |
C(-1,7/3) |
|
| 0 |
(-5*(0)+9)/6= 3/2 |
D(0,3/2) |
|
| 1 |
(-5*1+9)/6= 2/3 |
G(1,2/3) |
Si può giungere alle stesse conclusioni esplicitando rispetto alla x e scegliendo in maniera arbitraria i valori della y.